수소 원자에서 전자가 가질 수 있는 상태는 슈뢰딩거 방정식(Schoedinger Equation)을 풀어 얻을 수 있다.
이에 따르면 수소 원자에서 전자가 가질 수 있는 상태는 양자 수(quantum number)로 표현될 수 있는데, 각각의 양자 수가 가질 수 있는 값들은 다음과 같다.
$$ \begin{aligned} n & = 0, \; 1, \; 2, \; 3, \; 4, \; \cdots \\ l & = 0, \; 1, \; 2, \; \cdots, n-1 \\ m & = -l, \; \cdots, \; 0, \; \cdots, \; l \\ s & = + \frac{1}{2}, \; - \frac{1}{2} \end{aligned} $$
여기서 $n$은 주양자수(principal quantum number)라 불리며, 주양자수는 보어의 원자 모형에서 전자의 궤도 반지름을 결정한다.
수소 원자가 아닌 일반적인 원자들은 수소 원자보다 복잡한 상태를 갖지만, 그럼에도 불구하고 강하게 속박돼 있는 양이온과, 그 주변을 떠도는 전자로 근사해 마치 수소 원자처럼 기술할 수 있기 때문에 위에서 설명한 양자수들을 활용해 원자의 상태를 기술하는 것이 보통이다.
흔히 주양자수 $n$에 해당하는 상태들을 "$n$번째 껍질"이라고 부른다.
한편 궤도양자수 $l$은 역사적인 이유로 $l = 1,\;2,\;3,\;\cdots$ 대신 $s, \; p, \; d, \; f, \; g, \; \cdots $와 같이 로마자로 표기한다.
전자의 에너지는 주양자수 $n$과 궤도양자수 $l$이 결정하므로 자기양자수 $m$이나 스핀양자수 $s$는 원자의 상태를 기술할때 보통 생략된다.
실리콘(Si)의 원자번호는 14인데, 이는 원자핵에 양성자가 14개, 그 주위에 전자가 14개 존재한다는 의미이다.
바닥 상태(가장 낮은 에너지 상태)의 실리콘 원자를 위에서 설명한 표기법으로 기술하면 아래와 같다.
$$ 1s^22s^22p^63s^23p^2 $$
이 기호에서 첫번째의 $1s^2$는 $n=1$ 껍질에 $l=0$ 상태에 전자가 2개($m=0,\; s=\pm 1/2$) 있음을 의미한다.
이어지는 기호도 마찬가지로 이해할 수 있는데, 예를 들어 $2p^6$는 $n=2$ 껍질에 $l=1$ 상태에 전자가 6개($m= -1,\;0,\;+1,\; s=\pm 1/2$) 있음을 의미한다.

실리콘 원자의 세번째 껍질($n=3$)에서 가능한 상태의 수는 $s$오비탈($l=0$)의 2개($m=0$, $s=\pm 1/2$)와 $p$오비탈($l=1$)의 6개($m=-1,\;0,\;1$, $s=\pm 1/2$)로 총 8개이다.
(여기서 오비탈이란 전자의 파동함수를 의미하며, 전자의 확률분포라고 생각하면 된다.)
그러나 실리콘 원자가 가지는 총 14개의 전자들 중 10개의 전자를 이미 첫 번째와 두 번째 껍질을 채우는 데 써버렸기 때문에 세 번째 껍질에는 4개의 전자만이 있게된다.
아래 그림은 $s$오비탈과 $p$오비탈의 형태가 나타나 있다.
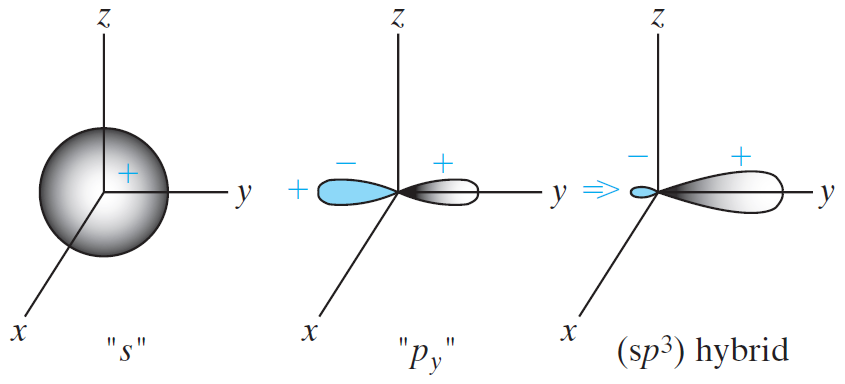
$s$오비탈은 모든 방향에 대해 대칭적인 구 형태이며, $p$오비탈은 호리병 모양을 하고 있다.
실리콘 원자가 고립돼 있으면 이상에서 설명한 오비탈을 가지게 된다.
그러나 다수의 실리콘 원자가 밀집되게 되면, 이들의 상호작용에 의해 오비탈의 형태가 달라지게 되는데, 위 그림에서와 같이 $s$오비탈과 $p$오비탈이 합쳐진 $sp^3$ hybrid 오비탈이라는 비대칭적인 방망이 형태가 된다.
만약 $N$개의 실리콘 원자가 모여있다면, 기존에 $2N$개의 $s$오비탈 상태와 $6N$개의 $p$오비탈 상태가 이제는 $8N$개의 $sp^3$ hybrid 오비탈 상태가 되는 것이다.

각각의 실리콘원자에 대해 $sp^3$오비탈들은 정사면체의 꼭지점 방향을 향하게 되며, 종국에는 위 그림과 같이 다른 실리콘 원자들과 결합을 이루어 앞서 설명한 다이아몬드 격자를 이루게 된다.
($8N$개의 전자 상태란 공간적인 분포 $4N$개에 스핀상태 $2$개의 곱인 것이다. 따라서 공간분포만 생각하면 각각의 원자들은 4 종류의 오비탈을 가지는 것이며 이들이 정사면체의 각 꼭지점 방향을 향하게 된다.)
여기서 결합이란 $sp^3$오비탈을 가지는 두 개의 원자가 하나의 양자역학적 시스템을 이룰때 아래 그림에 나타난 것처럼 두 가지의 상태가 가능한데, 이 중 bonding orbital 상태를 이루었음을 의미한다.

양자역학에서 기본입자들은 보손(boson)과 페르미온(fermion)이라는 두 가지 종류로 분류될 수 있는데, 전자는 페르미온(fermion)으로 분류되며, 페르미온의 특징은 여러 개의 입자들이 모였을때 입자들의 상태가 반대칭적(anti-symmetric)이 된다는 특징이 있다.
위 그림에서 두 전자의 오비탈이 antibonding 형태를 이루는 경우, 두 전자의 상태가 반대칭적이기 위해서는 두 전자의 스핀 상태가 동일해야 한다.
반면 두 전자의 오비탈이 bonding 형태를 이루는 경우, 두 전자의 상태가 반대칭적이기 위해서는 두 전자의 스핀 상태가 반대여야만 한다.
따라서 실리콘 원자들이 모여 다이아몬드 격자를 이룰 때, 각각의 원자에서 세 번째 껍질($n=3$)에 있는 4개의 전자들은 $sp^3$ 오비탈을 형성하며, 이들은 서로 이웃한 원자의 전자들과 bonding orbital결합을 이루고, 이때 반대칭적인 상태를 만들기 위해 결합에 참여한 두 전자는 스핀이 서로 반대인 상태가 된다.
실리콘이 결합할때 이웃한 원자들의 전자쌍이 bonding 오비탈을 형성하는 이유는, bonding 상태가 antibonding 상태보다 에너지적으로 더 선호되기 때문이다.
에너지적으로 더 선호된다는 것은 더 낮은 에너지를 갖는다는 의미이다.
물리학에서 보존력(conservative force)을 통해 상호작용하는 입자계에서는 입자들간의 상호작용이 입자들의 총 에너지를 낮추는 방향으로 형성됨이 알려져 있다.
따라서 입자계는 점차 낮은 에너지 상태로 갈 수밖에 없고, 이러한 이유로 물리학에서는 입자계가 낮은 에너지 상태를 선호한다고 말한다.
실리콘 원자가 단독으로 존재할 때, 원자핵 주위를 맴도는 전자들은 명확한 에너지를 가진다.
앞서 설명했듯이 전자들의 에너지는 주로 주양자수 $n$과 궤도양자수 $l$로 정해진다.
실리콘 원자에서 첫 번째와 두 번째 껍질에 속해있는 전자들은 강하게 속박되어 움직일 수 없는 상태이므로 에너지 관점에서 다른 원자들과의 상호작용에 거의 참여하지 않는다.
따라서 세 번째 껍질에 속하는 $s$오비탈과 $p$오비탈의 전자가 가지는 에너지가 중요해 지는데, 아래의 그림의 오른쪽 끝단에는 바로 이 두 오비탈이 가지는 명확한 값으로 정의된 에너지가 표현돼 있다.

그런데 실리콘 원자가 단독으로 존재하는 것이 아닌, 다수의 원자가 서로 가까이 다가갈 경우, 앞서 설명했던 $sp^3$오비탈의 형성과 함께 bonding 결합이 나타나게 된다.
이 과정을 에너지적으로 살펴보면 위의 그림에 나타난 것처럼, 모든 원자들이 기존에 완벽하게 동일한 값으로서 가지던 $s$오비탈과 $p$오비탈의 에너지값이 원자들이 서로 상호작용을 함에 따라 분화(split)되기 시작한다.
이는 양자역학에서 말하는 파울리 배타원리의 결과 혹은, 앞서 설명한 bonding과 antibonding 상태로 이야기할 수 있는데, 전자들은 하나의 상태에 한 개의 전자만 있을 수 있는 페르미온들이기 때문에 다수의 전자들의 에너도가 완벽히 동일한 값일 수가 없는 것이다.
이러한 에너지 분화로 한때 $s$오비탈과 $p$오비탈이었던 전자들의 에너지는 하나의 영역으로 통합되었다가, 안정적인 $sp^3$오비탈을 형성하면서 위 그림에 나타난 것 처럼 격자 간격이 $5.43$옹스트롬 정도가 되었을 때에는 두 개의 영역으로 분리된다.
실리콘 원자들이 단독으로 존재할때 3번째 껍질에 존재하던 총 $8N$개의 상태들은 실리콘 원자들이 격자를 이루었을때는 최종적으로 $4N$개의 Valence band와 $4N$개의 Conduction band라는 두 개의 부류로 에너지적으로 분리되며, 이 두 band 사이에는 전자가 있을 수 없는 에너지 영역이 생기게 되는데 이를 밴드갭(bandgap)이라고 부른다.
실리콘 결정의 경우, 밴드갭은 상온에서 약 1.1eV 정도이다.
에너지에 관해서 살펴본 이상의 결과들은 격자 구조에 대한 슈뢰딩거 방정식을 풀어 얻을 수 있는 결과들이다.
다음 글에서는 이와 관련해 Bloch의 정리와 First Brillouin Zone, 그리고 전자의 유효 질량(effective mass)에 대해 살펴보도록 하겠다.
'물리학(Physics)' 카테고리의 다른 글
| 갈릴레이의 상대성 원리 (0) | 2022.01.22 |
|---|---|
| 결정 속 전자의 운동 (0) | 2021.03.06 |
| 결정(Crystalline Materials) (0) | 2021.02.26 |
| 패러데이 법칙과 운동 기전력, 로런츠 힘의 관계 (0) | 2020.12.05 |
| 유한 퍼텐셜 우물의 산란 (0) | 2020.11.21 |